1 矩阵置零
难度:中等
题目描述
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素置为0。
示例 1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2:

输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
进阶:
一个直观的解决方案是使用
O(mn)的额外空间,但这并不是一个好的解决方案。一个简单的改进方案是使用
O(m + n)的额外空间,但这仍然不是最好的解决方案。你能想出一个仅使用常量空间的解决方案吗?
思路 - 初见
遍历两遍,用两个哈希表分别存储要置零的行和列,第一遍记录非重复的为零的数所在的行和列并存储,第二遍根据哈希表置零
你的思路完全正确!这属于标准的 $O(M+N)$ 空间复杂度 解法。
虽然你提到了“哈希表”,但在实际工程和面试中,因为行号和列号是连续的整数(0 到 N-1),使用 boolean 数组 代替哈希表(HashSet)效率会更高,内存占用也更小,但逻辑核心完全一致。
以下是基于你的思路优化的代码实现:
代码 - 初见
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
// 使用两个 boolean 数组代替哈希表
// 记录哪些行需要置零
boolean[] rowFlags = new boolean[m];
// 记录哪些列需要置零
boolean[] colFlags = new boolean[n];
// 第一遍遍历:找出所有为 0 的位置,并标记对应的行和列
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
rowFlags[i] = true;
colFlags[j] = true;
}
}
}
// 第二遍遍历:根据标记将元素置零
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 只要当前行 OR 当前列被标记过,就置零
if (rowFlags[i] || colFlags[j]) {
matrix[i][j] = 0;
}
}
}
}
}改进
既然我们不能开新的数组来记录哪行哪列要变 0,那我们就征用原矩阵的第一行和第一列来做标记。
逻辑步骤:
存状态:因为第一行和第一列要被征用,所以首先要检查它们原本是不是包含 0,用两个变量
row0Flag和col0Flag记下来。做标记:遍历剩下的矩阵(从
(1,1)开始)。如果发现matrix[i][j] == 0,就去修改它的“表头”:
让
matrix[i][0] = 0(告诉第一列:这行废了)让
matrix[0][j] = 0(告诉第一行:这列废了)置零:根据第一行和第一列的标记,把中间的元素置零。
恢复表头:最后根据第 1 步存的 flag,决定要不要把第一行和第一列全变 0。
代码 - 改进
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
boolean row0Flag = false;
boolean col0Flag = false;
// 1. 检查第一列是否有 0
for (int i = 0; i < m; i++) {
if (matrix[i][0] == 0) {
col0Flag = true;
break;
}
}
// 2. 检查第一行是否有 0
for (int j = 0; j < n; j++) {
if (matrix[0][j] == 0) {
row0Flag = true;
break;
}
}
// 3. 遍历其余部分,将 0 的信息“投影”到第一行和第一列
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = 0; // 标记该行
matrix[0][j] = 0; // 标记该列
}
}
}
// 4. 根据第一行和第一列的标记,将内部元素置零
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
// 只要行头或列头是 0,这个位置就得是 0
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
// 5. 最后处理第一行和第一列
if (row0Flag) {
for (int j = 0; j < n; j++) matrix[0][j] = 0;
}
if (col0Flag) {
for (int i = 0; i < m; i++) matrix[i][0] = 0;
}
}
}2 螺旋矩阵
难度:中等
题目描述
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:

输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]思路 - 初见
记 k 为min(m,n),循环k,向右走m-k,向下走n-k,然后左走m-k,最后上走n-k-1,k++
未实现
你的思路大方向是对的(按层模拟),这被称为**“按层遍历”**。但是,试图通过计算具体的“步数”(如
m-k,n-k)来控制循环,在代码实现上会非常痛苦,极容易遇到以下两个坑:
步数缩减规律:每一圈走完,长和宽其实是各减 2,而不是减 1。
中心死角:当矩阵不是正方形(如 $3 \times 5$),或者剩下最后一行/一列时,用步数控制很难判断是否该停下来,容易导致重复访问或越界。
✅ 更优思路:设定四个边界 (Simulation with Boundaries)
与其计算“要走几步”,不如设定上、下、左、右四面墙。
每走完一条边,就将对应的墙向内收缩(比如走完第一行,上墙就下移一格)。当墙壁撞在一起时,结束循环。
这种方法不需要复杂的数学公式计算步数,逻辑非常直观。
代码
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> res = new ArrayList<>();
if (matrix.length == 0) return res;
// 1. 设定四个边界
int top = 0;
int bottom = matrix.length - 1;
int left = 0;
int right = matrix[0].length - 1;
// 2. 循环直到边界交错
while (true) {
// ---> 向右走 (从左边界到右边界)
for (int i = left; i <= right; i++) res.add(matrix[top][i]);
// 走完第一行,上边界下移。如果越过下边界,说明结束
if (++top > bottom) break;
// ↓ 向下走 (从上边界到下边界)
for (int i = top; i <= bottom; i++) res.add(matrix[i][right]);
// 走完最右列,右边界左移。如果越过左边界,说明结束
if (--right < left) break;
// <--- 向左走 (从右边界到左边界)
for (int i = right; i >= left; i--) res.add(matrix[bottom][i]);
// 走完最下行,下边界上移
if (--bottom < top) break;
// ↑ 向上走 (从下边界到上边界)
for (int i = bottom; i >= top; i--) res.add(matrix[i][left]);
// 走完最左列,左边界右移
if (++left > right) break;
}
return res;
}
}3 旋转图像
难度:简单
题目描述
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:

输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:

输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
思路 - 初见
从第i层开始,第j行,(1,1)放到(1,n),将(1,n)取出,放到(n,n),然后(n,n)放到(n,1),1可替换为j,i>n/2时终止
代码 - 初见
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// 1. 枚举层数 (i):从外向内,只需遍历到 n/2
for (int i = 0; i < n / 2; i++) {
// 2. 枚举当前层的元素位置 (j)
// j 的范围是 [i, n - 1 - i)
// 注意:左闭右开,因为每一行的最后一个点是下一条边的起始点,不能重复交换
for (int j = i; j < n - 1 - i; j++) {
// 暂存左上角 (对应你说的 1,1)
int temp = matrix[i][j];
// ⚠️ 逆时针寻找源头,把值填入目标位置
// 左上角 = 左下角
// 对应坐标:(i, j) = (n-1-j, i)
matrix[i][j] = matrix[n - 1 - j][i];
// 左下角 = 右下角
// 对应坐标:(n-1-j, i) = (n-1-i, n-1-j)
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
// 右下角 = 右上角
// 对应坐标:(n-1-i, n-1-j) = (j, n-1-i)
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
// 右上角 = temp (原左上角)
// 对应坐标:(j, n-1-i) = temp
matrix[j][n - 1 - i] = temp;
}
}
}
}4 搜索二维矩阵 II
难度:中等
题目描述
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例 1:
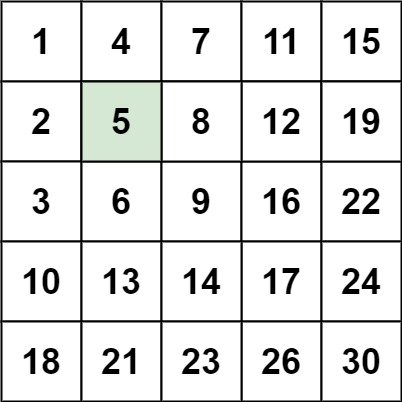
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true示例 2:
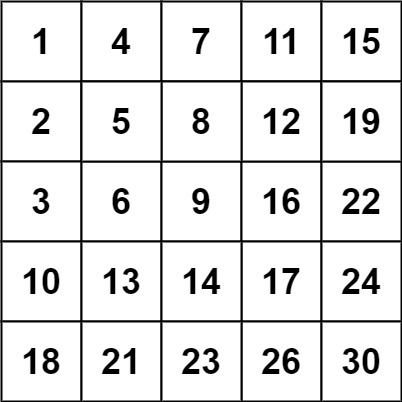
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109
思路 - 初见
二分查找,找到斜对角一边小一边大的时候,分别检查行列,没有找到就返回false,找到就返回true,思路模糊,代码不好写
🚀 核心思路:把矩阵看作“二叉搜索树”
不要从左上角((0,0))开始找,因为往右和往下都是变大,方向不确定。 我们要找一个“岔路口”,即一个方向变大,一个方向变小的位置。
最佳起点:右上角 (0, n-1)
往左走:数值一定变小。
往下走:数值一定变大。
这样,每一次比较,我们都能排除掉一行或者一列,就像剥洋葱一样,直奔目标。
📝 算法流程
指针停在右上角
(row = 0, col = n - 1)。如果
current > target:说明当前列下面的数都比它大,肯定也比 target 大,所以整列排除,指针向左移 (col--)。如果
current < target:说明当前行左边的数都比它小,肯定也比 target 小,所以整行排除,指针向下移 (row++)。如果
current == target:找到了,返回true。如果指针跑出边界还没找到:返回
false。
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0) return false;
// 1. 起点定在右上角
int row = 0;
int col = matrix[0].length - 1;
// 2. 只要不越界,就持续搜索
while (row < matrix.length && col >= 0) {
int current = matrix[row][col];
if (current == target) {
return true; // 找到了
} else if (current > target) {
// 当前值太大 -> 往左走(变小)
col--;
} else { // current < target
// 当前值太小 -> 往下走(变大)
row++;
}
}
// 3. 走出边界还没找到
return false;
}
}
